A Sip of Monstrous Moonshine

You and a stranger have been instructed to meet up sometime tomorrow, somewhere in New York City. You (and the stranger) can decide for yourselves when and where to look for each other. But there can be no advance communication. Where do you go?

Me, I’d be at the front entrance to the Empire State Building at noon, possibly missing my counterpart, who might be under the clock at Grand Central Station. But, because there are only a small number of points in New York City that stand out as “extra-special”, we’ve at least got a chance to find each other.

A Schelling point is something that stands out from the background so sharply that we can expect people to coordinate around it. Schelling points are on my mind this week, because I’ve just heard David Friedman give a fascinating talk about the evolution of property rights, and Schelling points play a big role in his story. But that story is not the topic of this post.

Instead, I’m curious about the Schelling points that say, two mathematicians, or two economists, or two philosophers, or two poets, or two street hustlers might converge on. Suppose, for example, that you asked two mathematicians each to separately pick a number between 200 and 300, with a prize if their answers coincide. I’m guessing they both go for 256, the only power of two within range.

What about, say, numbers between 1000 and 2000? Historians might converge on 1066; (American) accountants on 1040. But for mathematicians, the obvious Schelling point would be 1729, the smallest number that can be written as the sum of two cubes in two different ways. (It’s 9³+10³, but it’s also 12³+1³). The reason we’re likely to jump at this number is that we were all brought up on the famous story of G.H. Hardy‘s visit to Ramanujan‘s deathbed:

Hardy used to visit him, as he lay dying in hospital at Putney. It was on one of those visits that there happened the incident of the taxicab number. Hardy had gone out to Putney by taxi, as usual his chosen method of conveyance. He went into the room where Ramanujan was lying. Hardy, always inept about introducing a conversation, said, probably without a greeting, and certainly as his first remark: ‘I thought the number of my taxicab was 1729. It seemed to me rather a dull number.’ To which Ramanujan replied: ‘No, Hardy! No, Hardy! It is a very interesting number. It is the smallest number expressible as the sum of two cubes in two different ways.

(This version is from C.P. Snow‘s introduction to Hardy’s brief autobiography A Mathematician’s Apology. If you’ve never read this book, you should not read another thing until you’ve filled this gap — and I envy you the magical experience you’re about to have!)

In a somewhat higher range, the clear Schelling point is 196883. This one’s a little harder to explain, but here’s a brief (and necessarily imperfect) overview: One of the great accomplishments of the 1970s and 1980s was a complete classification of all the possible ways in which an object can be symmetric. (Actually, I’ve already oversimplified; the classification covers only the “simplest” kinds of symmetries, which in turn are known to be the building blocks of all other symmetries. There are still plenty of open questions about how many ways those building blocks can be joined together).

Most of these symmetries fit into natural families (like the family consisting of the symmetries of a triangle, the symmetries of a square, the symmetries of a pentagon and so on). But a few stand alone, and the one that stands most strikingly alone is the so-called “monster” symmetry. If you live in three or four dimensions like the rest of us, then you’ve never seen an object with this kind of symmetry, because it first manifests itself in a space with 196,883 dimensions.

Now let’s forget about symmetry for a moment and talk about something else entirely. One of the most important functions in number theory is the “elliptic modular function”, which starts out like this:

Notice the 196884? Notice how close it is to 196883? Sort of a curious coincidence, no?

Here’s another coincidence: 21493760 is 196884 + 21296876. Guess what’s the next higher dimension in which the monster symmetry occurs? It’s 21296876.

And on it goes. The next term in the elliptic modular function is 864299970 q³ And we can write 86429970 = 842609326 + 21296876 + 196883 + 196883 + 2. Except for that 2, the numbers on the right are all dimensions in which the monster symmetry occurs. There are similar suggestive patterns for all the other coefficients of the elliptic modular function.

These “coincidences” are so extraordinary that they can’t possibly be coincidences, but tracking down their sources turned out to be one of the great adventures of 20th century mathematics. The hero of that quest was Richard Borcherds who managed to figure out what was going on using, of all things, ideas that come from string theory, a branch of mathematical physics that has, on the surface, as little to do with monster symmetries and the elliptic modular function as they have to do with one another.

All of which goes to explain why I sometimes wear a t-shirt that says

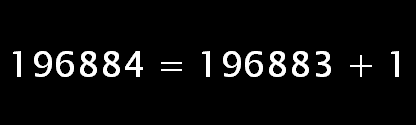
Not many people understand it, but when someone does, we know instantly that we have something in common.

What are the Schelling points for the people who share your hobby or profession? What numbers, places, or things could you count on a fellow practitioner to see as the “obvious” choices?